회전곡면의 넓이
\(\) \(y=f(x)\) 꼴의 함수를 \(y\)축을 중심으로 회전해 만들어진 곡면의 넓이는 어떻게 구할 수 있을까?
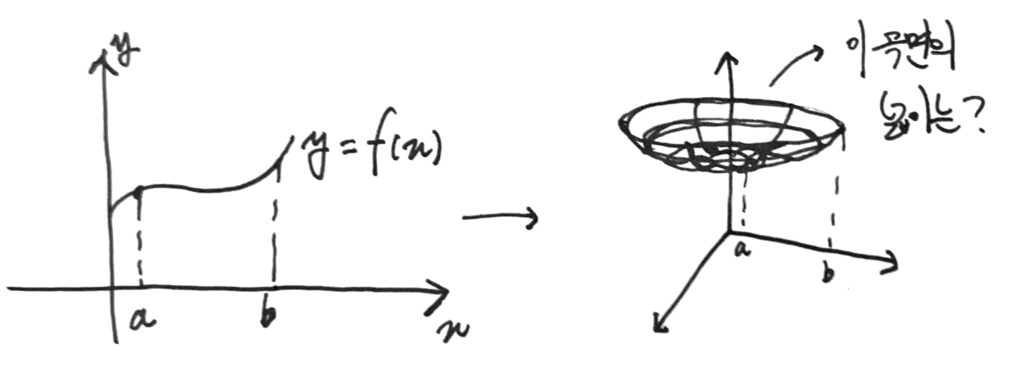
문제를 간단하게 해결하기 위해, \((r, \theta , z)\)1를 성분으로 가지는 원기둥 좌표계를 사용하자. 회전시키고자 하는 일변수함수는 \(z=f(r)\)로 정의한다.
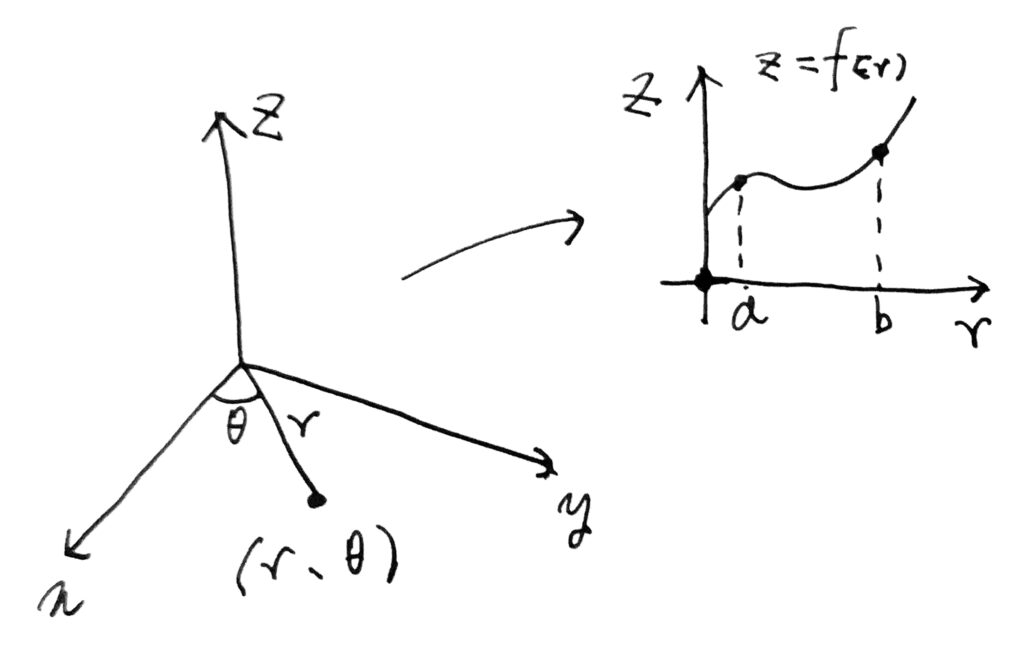
회전 시 \(r\)의 범위를 \([a, b]\), \(\theta\)의 범위를 \([\theta_0, \theta_1]\)으로 두었을 때, 회전곡면 \(X(r, \theta)\)는 아래의 그림과 같이 \(X(r, \theta) = (r\cos\theta , r\sin\theta , f(r))\)으로 매개화할 수 있다.
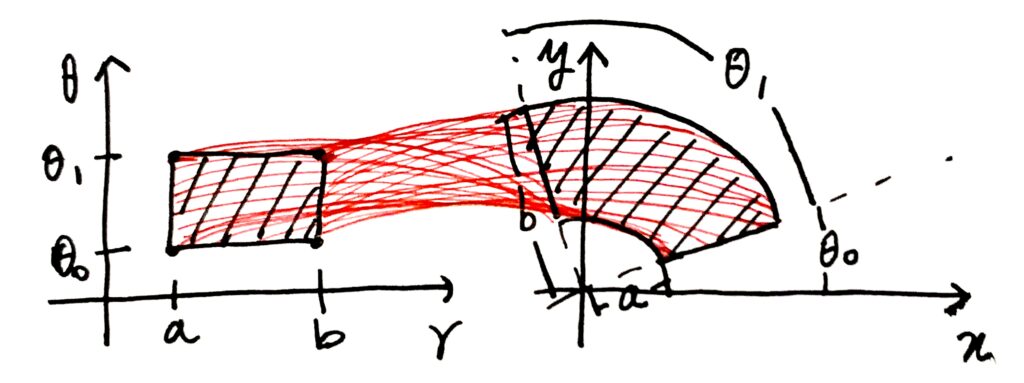
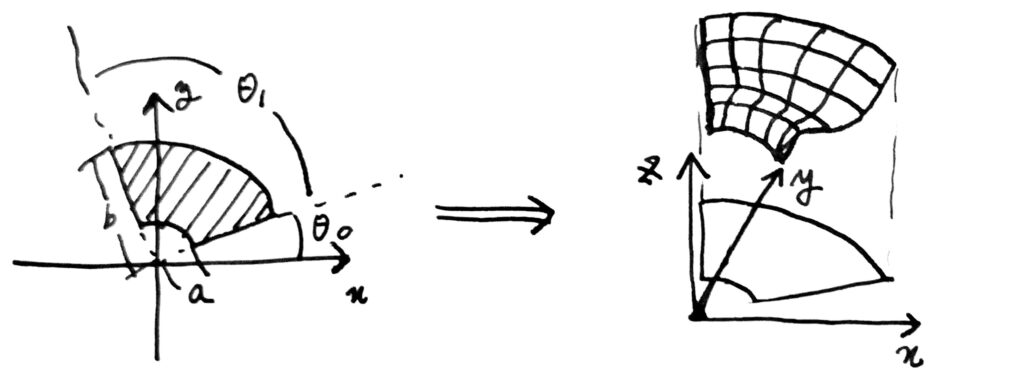
이때, 특정 \(r, \theta\)에서의 곡면의 미소 면적(면적소) \(dS\)를 구하자. 면적소는 아래 그림과 같이, 곡면을 각 매개변수에 대해 편미분한 벡터장(이는 곡면의 접방향을 나타낸다)의 외적의 절댓값2에, 두 매개변수의 미소변화량을 곱한 것으로 정의된다.
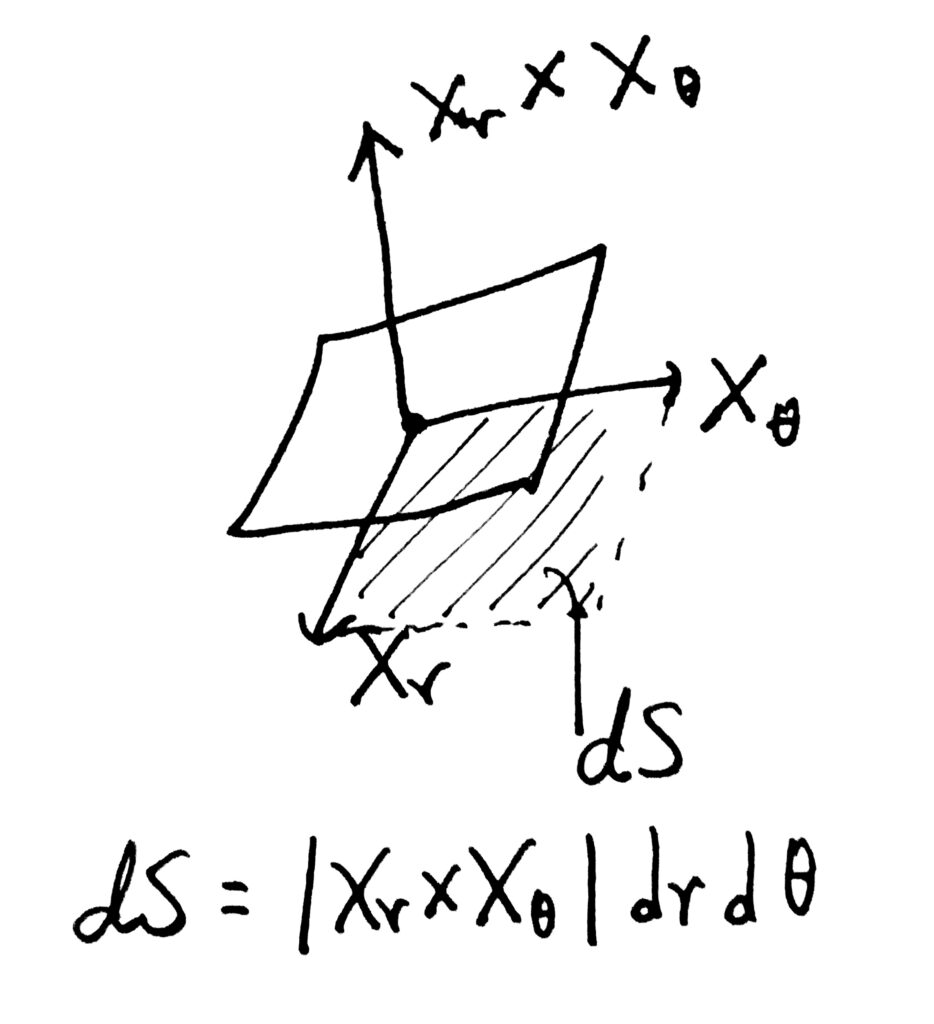
면적소의 계산 과정은 다음과 같다.
\(\begin{cases} X_r(r, \theta) = (\cos\theta , \sin\theta , f'(r)) \\ X_{\theta}(r, \theta) = (-r\sin \theta, r\cos\theta, 0) \\ \end{cases}, \ |X_r \times X_{\theta}| = \begin{Vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ \cos\theta & \sin\theta & f'(r) \\ -r\sin \theta & r\cos\theta & 0 \\ \end{Vmatrix} = r\sqrt{(f'(r))^2 + 1}\)
\(\therefore dS = r\sqrt{(f'(r))^2 + 1}drd \theta \)
곡면의 면적은 곧, 매개곡면의 정의역에서 면적소를 적분한 것이므로, 다음 식을 얻는다. 이 식을 통해, 주어진 함수에 따라 적절한 적분 방법을 이용하여 면적을 구할 수 있다.
\(\therefore S = \int^{\theta_1}_{\theta_0}{\int^b_a{r\sqrt{(f'(r))^2 + 1}drd \theta}}\)